0. 들어가며
나는 이번 학기 내내 회귀분석 공부를 나름 열심히 했다고 자부한다. 하지만 ‘교수님이 가르쳐준 지식을 100% 흡수할 수 있었는가’ 묻는다면 고개를 저을 수밖에 없었다. 회귀분석은 그만큼 어려운 과목이었고, 특히나 R프로그램을 이번 과목에서 처음 사용해보는 내 입장에서는 두 배 더 어려웠다. 그래도 ‘데이터사이언스융합전공’이라는 내 다전공에 맞게 데이터 분석 방법을 알 수 있어서 매우 좋은 시간이었고, 기말 프로젝트 발표 준비를 진행할 때도 나름 즐겼던 기억이 있다. 지금부터는 내가 미처 10페이지 안에 정리하지 못했던, 어떤 과정을 거쳐서 기말 프로젝트를 진행했는지 정리하는 시간을 갖도록 한다. 다만 코드는 자제해달라는 교수님의 답변에 따라 공개하지 않는다.
+추가
보고서 정리를 마무리한 뒤 티스토리로 옮겨서 작성하는데 워드의 수식이 입력되지 않는다는 심각한 사실을 발견했다. 다른 방법을 이용해서 R에서 사용하는 수식작성법을 사용할 수 있는 듯 하지만, 여기에 입력된 수식이 꽤 많아 솔직히 매우 귀찮기 때문에 임시로 각 수식을 sum, sqrt와 같이 영어로 입력하여 정리하도록 한다.
1. 주제 : 응답자의 평일 수면시간과 체감 스트레스, 체감 우울감이 주말 수면시간에 미치는 영향 분석
2. 팀원 : 1명
3. 프로젝트 기간 : 기말고사 대체 (2021년 12월 1일 ~ 2021년 12월 17일(발표))
4. 수행절차
수행절차는 크게 I. 서론, II. 본론, III. 결론 부분으로 나뉜다. 그리고 본론은 크게 (1) 회귀모형의 설립 단계와 (2) 회귀모형의 검정으로 나눌 수 있는데, 이를 세분화하여 나열하면 아래와 같다.
(1) ① 변수 선택 - ② 중회귀모형의 설립 - ③ 가설의 검정
(2) ④ 회귀계수의 검정 - ⑤ 적합결여검정 - ⑥ 분산 및 정규성의 안정화를 위한 변수변환 - ⑦ 다중공산성의 탐색과 조정 - ⑧ 잔차 검정 - ⑨ 이상치 제거 후 잔차의 재검정 - ⑩ 예측력 판단
기말프로젝트 보고서에는 ‘10페이지 제한’으로 인해 상세한 내용을 담지 못했었다. 그러므로 블로그에는 내가 어떤 내용을 분석했는지만 적는 것이 아닌, 왜 이렇게 분석했는지 상세하게 작성하는 것을 목표로 한다.
자료의 경우, 2019년 국민건강영양조사 자료를 제공받아 사용하였으며 분석은 R을 사용하였다.
번호의 단계는 I (1) ① (가) 순이다.
Ⅰ. 서론
(1) 연구주제 배경
사람은 성인을 기준으로 평균 7 ~ 9시간 정도 수면을 취하는 것이 건강에 좋다고 말한다. 하지만 학업이나 직장 업무를 하다 보면 어쩔 수 없이 잠을 뒷전으로 미루고 그 일을 모두 끝내야 하는 경우가 있다. 나 또한 비슷한 이유로 잠을 줄여가면서 업무를 끝내려고 하는 경우가 종종 있었다. 나는 대신 주말에는 반드시 10시간 이상 자려고 하는데, 이를 두고 소위 ‘몰아서 잔다’라고 말한다. 몰아서 자는 행동은 생체리듬을 깨뜨려 건강에 좋지 않을 것 같지만 마냥 그렇지도 않다. 평소 잠을 충분히 자지 못한 경우에는 오히려 평일에 쌓인 피로를 풀어 건강에 도움을 줄 수 있고 비만도 예방할 수 있다는 연구결과가 존재하는 만큼 생각보다 유의미한 행동이다 1. 따라서 나는 국민건강영양조사의 자료를 통해 ‘몰아서 자는’ 사람들이 보편적인 행동인지를 확인해보고자 한다.
나는 응답자의 평일 수면시간과 주말 수면시간만을 가지고 단순회귀분석을 할 경우, 프로젝트 분석 결과를 보여줄 것이 많이 없다고 판단하여 인터넷 기사를 이용한 추가 조사를 진행하였고 의미 있는 자료를 많이 찾을 수 있었다. 특히 내 이목을 끈 자료는 스트레스가 많을수록 하루 수면 시간이 적다는 연구결과였는데 2, 나는 여기에 더하여 우울감과 수면시간과의 연관성도 확인해보면 재미있는 결과를 얻을 수 있지 않을까 하는 생각이 들었다. 따라서 나는 “응답자의 평일 수면시간과 체감 스트레스, 체감 우울감이 주말 수면시간에 미치는 영향”을 분석하기로 결정하였다.
(2) 가설 설정
나는 이 연구를 진행하기에 앞서 세 가지의 가설을 설정하였다.
첫째, 주말 수면시간과 평일 수면시간은 서로 반비례의 관계일 것이다. 즉, 주말 수면시간이 증가할수록 평일 수면시간은 감소할 것이다. 이는 주말에 잠을 몰아서 자는 사람이 보편적이라는 의미를 내포하고 있다.
둘째, 주말 수면시간과 체감 스트레스는 서로 반비례의 관계를 나타낼 것이다. 즉, 체감 스트레스가 증가할수록 주말 수면시간이 감소할 것이다. 이는 스트레스가 많을수록 수면시간이 적어진다는 기사의 내용을 참고하였다.
셋째, 주말 수면시간과 체감 우울감은 서로 반비례의 관계일 것이다. 즉, 체감 우울감이 증가할수록 주말 수면시간은 감소할 것이다. 이는 우울감의 원인이 스트레스라는 보편적인 사실에 더하여 스트레스가 많을수록 수면시간이 적어진다는 기사의 내용을 참고하였다.
Ⅱ 본론
본론에서는 (1) 회귀모형을 구성하는 과정과 (2) 회귀모형을 검증하는 과정으로 나누어 정리한다. 이번 회귀분석에서 사용한 변수는 총 4개로, 설명변수 3개와 반응변수 1개로 구성되어 있다. 자세한 내용은 아래 표로 정리된 바와 같다.
| 변수 | 내용 | 값 유형 | 비고 |
| X1 | 주중(또는 일하는 날) 하루 평균 수면시간 | 숫자 (단위 : 시간) |
|
| X2 | 평소 스트레스 인지 정도 | 범주형 데이터 | 0 = “거의 느끼지 않는다” ~ 3 = “대단히 많이 느낀다. |
| X3 | 2주 이상 연속 우울감 여부 | 범주형 데이터 | 0 = “아니오” ~ 1 = “네” |
| Y | 주말(또는 일하지 않는 날, 일하지 않는 전날) 하루 평균 수면시간 | 숫자 (단위 : 시간) |
여기서 한 가지 언급할 점은, X2와 X3는 약간의 순서를 바꾸어 값을 수정하였다는 사실이다. 본래 원시자료를 살펴보면 X2는 1 = “대단히 많이 느낀다” ~ 4 = “거의 느끼지 않는다”였으며, X3도 1 = “네” ~ 2 = “아니오”였다. 그런데 일부러 위와 같이 값을 변경한 이유는 ‘기준 범주’ 때문이다. 범주형 데이터는 ‘기준 범주’과 ‘현재 범주’의 차이를 가지고 해석에 적용한다. 예컨대 ‘아니오’가 기준 범주이고, ‘예’가 현재 범주, 그리고 증감값이 α라고 가정한다면, 회귀분석 결과를 해석할 때 “아니오(기준범주)에 비해서 네(현재범주)일 경우 값이 α만큼 증가한다”라고 말한다. 이때 “있음”을 기준으로 하고 “없음”을 해석하는 것보다는 “없음”을 기준으로 “있음”을 해석하는 편이 더 용이할 것이라 판단하였다. 따라서 모든 범주형 값을 “없음”부터 “있음”으로 나타내도록 통일성 있게 수정하였다.
데이터는 N/A로 표시되는 결측치와 ‘비해당’, ‘응답’과 같은 값은 모두 제거하였다. 또한 ‘주중 수면시간’과 ‘주말 수면시간’ 변수에서 현실적으로 불가능한, 혹은 비성실한 대답이라고 판단되는 값은 제거하였다. 예컨대 주중 수면시간 혹은 주말 수면시간이 2시간 이하이거나, 15시간 이상인 데이터는 모두 제거하였다. 이러한 전처리를 거쳐서 8110개의 데이터 중 6648개의 데이터를 확보할 수 있었으며, 이들을 대상으로 회귀분석을 진행하였다.
(1) 회귀모형의 설립
① 변수 선택
회귀모형을 세우기 이전, 나는 먼저 내가 선정한 변수가 모두 유의한지 확인하기 위해서 ‘변수선택’을 진행하였다. 차후 회귀분석을 진행할 때 설명변수와 반응변수 간 관계 유의성을 검증하는 과정을 생략하고, 효율적으로 회귀모형을 세우기 위함이었다. 나는 변수 선택의 당위성을 확보하기 위해서 내가 사용할 수 있는 모든 방법을 적용하였다.
(가) 모든 가능한 회귀 – 수정된 결정계수

‘수정된 결정계수’는 회귀모형의 설명력을 나타낸다. 수정된 결정계수가 높을수록, 우리는 해당 회귀모형이 데이터의 추이를 잘 설명하고 있다고 말할 수 있으며, 이는 곧 수정된 결정계수가 높을수록 해당 회귀모형이 최적이라는 사실을 나타낸다고도 볼 수 있을 것이다. 다만, 수정된 결정계수가 낮다고 해서 해당 회귀모형이 의미 없다고 치부하는 건 옳지 않다. 뒤에서 다룰 잔차의 가정이 잘 만족한다면 결정계수의 값이 낮더라도 통계적으로 유의미하게 해석할 수는 있다. 변수 선택 경우의 수에 따라서 회귀계수를 도출한 결과 ‘모든 변수를 사용하여 회귀모형을 구성한 경우’가 최적의 모형이라는 사실을 확인할 수 있었다. 그러나 회귀분석에서는 모형을 단순화하는 것도 굉장히 중요하게 생각하고 있어 기준에 미치지 못하더라도 연구자의 주관에 따라 선택 혹은 기각하는 경우가 있다. 위 경우에서도 연구자의 주관에 따라서 3개의 변수를 사용하여 0.4266의 결정계수를 도출하는 것보다는 1개의 변수만을 사용하여 0.4206의 결정계수를 도출하는 편을 선호할 수도 있다.
(나) 모든 가능한 회귀 – 맬로우즈 Cp

맬로우즈 Cp는 단순히 말하면 모형의 정밀도를 기준으로 최적의 모형을 찾는 방법이다. 맬로우즈 Cp값이 사용된 변수의 개수에 수렴할수록, 해당 모형은 최적이라고 본다. 그래프 아래 표 두 번째 줄은 맬로우즈 Cp값을, 세 번째 줄은 사용된 변수의 개수를 보여주고 있다. 해당 그래프만 보면 당연히 ‘모든 변수를 사용한 회귀모형’이 가자 적합하다고 이야기할 수 있겠으나, 여기에는 맬로우즈 Cp의 함정이 숨어있다. 맬로우즈Cp값은 완전모형일 때 반드시 (변수의 개수)로 수렴한다는 특성이 존재하기 때문이다. 즉, 마지막 그래프가 4로 수렴하는 이유는 그 모형이 적합해서가 아니라 맬로우즈 Cp의 특성에 의해 ‘완전 모형에서 사용된 변수 개수’인 4로 나타났기 때문으로 보아야 정확하다.
가장 눈에 띄는 모형은 1번, 4번, 5번, 7번 모형으로, 그나마 4번 모형이 사용된 변수 개수인 3에 근접했기 때문에 적합하다고 해석할 수도 있다. 다만 나는 7번 모형을 제외하고 나머지 모형을 고려했을 때, 가장 적은 값을 나타내는 4번 모형도 기준선인 3보다 훨씬 큰 값을 보여주고 있으므로, 모든 모형을 기각한 후 7번 모형을 차선책으로 채택하기로 결정하였다.
(다) 모든 가능한 회귀 – BIC

솔직히 말해, 변수 선택 방법 중 BIC에 대해서만큼은 교수님께서 해주신 말씀을 전부 이해하지는 못했다(아직 학부생 수준이라 많은 부분을 설명해주시지 않으셨을 가능성도 있다. 물론 내 희망사항이다). 따라서 아는 수준 내에서만 이야기하도록 한다.
BIC와 뒤에 나올 AIC는 최대가능도추정량θ_MLE을 활용하는데, θ_MLE는 L(θ_hat)을 최대화하는 θ값으로, L(θ)이 클수록 좋은 모형이라고 본다. 우리가 사용하는 BIC의 공식은 -2logL(θ_hat)+plog(n)이다. 즉, L(θ_hat)가 클수록 BIC는 작아지도록 설계되어 있으므로 BIC는 작을수록 최적의 모형이라고 본다. 참고로 plogn는 벌칙항이다. L(θ_hat)의 값은 구조상 설명변수가 많아질수록 값이 커지게 설계되어 있다. 그러므로 만약 이 벌칙항이 존재하지 않다면 설명변수가 많다는 이유만으로 최적의 모형이 되어버릴 것이다. 따라서 설명변수가 많아질수록 값이 커지는 plogn을 추가하여, 설명변수의 값이 많아질수록 값이 작아지도록 설계된 -2logL(θ_hat)의 단점을 극복하였다. BIC는 주로 변수를 단순화하는데 자주 사용된다.
위 값을 살펴보면 ‘모든 변수를 사용한 회귀모형’의 BIC가 -3665.3으로 가장 작은 값을 보여주고 있었다. 다만 모형의 단순화 측면에서 살펴보면 1번 모형과 4번 모형도 충분히 괜찮은 값을 보여주고 있다고 생각한다. 그래도 나는 단순하게 “BIC가 가장 작은 것을 최적의 모형으로 사용하자”라고 결정했기에 7번 모형을 최적의 모형을 선택하였다. 이러한 결정이 가능했던 이유는 애초에 사용한 변수가 적었기 때문이기도 하다. 만약 변수가 10개 이상이라면 1번과 4번 같이 변수가 적게 사용된 모형을 골라도 무방할 것이라 생각했다.
(라) 모든 가능한 회귀 – PRESSp

PRESS는 i번째 데이터를 삭제한 나머지를 가지고 회귀모형을 구성한 후 실제 i번째 값과 추정된 i번째 값의 차를 제곱한 값이다. 공식으로 나타내면 sum((yi - yi_hat)^2)이다. 만약 회귀모형이 데이터 값의 추이를 잘 예측한다면 당연히 (실제 i번째 값) – (추정된 i번째 값)의 차이는 작을 것이다. 따라서 PRESS는 현재 모형의 예측도를 나타내며, 값이 작을수록 최적의 모형이라고 본다.
위의 값을 살펴보면 2번 모형과 5번, 6번, 8번 모형이 PRESS값이 낮으므로 괜찮은 모형이라고 볼 수 있을 것이다. 이는 ‘수정된 결정계수’, ‘맬로우즈 Cp’, ‘BIC’에서 나타내는 결괏값과 비슷한 추이를 보여주고 있다. 그래도 가장 최적의 값을 보여주고 있는 모형은 어느 척도로 살펴보더라도 ‘완전 모형’을 가리키고 있으므로, 우리는 8번 모형을 최적의 모형으로 선택한다.
(마) 모든 가능한 회귀 – 완전모형 vs null_model
위 척도를 통해 선택한 완전 모형과 Y = 1로 이루어진 null_model을 부분 F검정을 통해 비교해보았다. H0 : β1=0, β2=0, β3=0, Ha : notH0 로 가설을 설정한 뒤 부분F검정을 실시한 결과 p값이 0.05를 넘지 못하면서 귀무가설을 기각하였다. 따라서 완전모형이 유의하다는 결과를 얻을 수 있었다. 따라서 ‘모든 가능한 회귀’방식을 사용하였을 때, Y= β0+ β1X1+ β2X2+ β3X3 + εi가 가장 최적의 모형임을 확인할 수 있었다.
(바) 단계별 회귀
다음에는 단계별 회귀를 살펴보고자 한다. 단계별 회귀는 전진 선택법, 후진 제거법과는 다르게 복잡한 메커니즘을 갖고 있다.
1단계 : 상수항만 존재하는 모형부터 시작한다. F값이 가장 큰 설명변수를 기존 회귀모형에 하나 추가한 뒤 부분F검정을 실시한다. 귀무가설을 기각할 경우 변수가 추가되며, 그렇지 않으면 현재 모형을 유지한다. (추가된 설명변수가 X2라고 가정한다)
2단계 : 추가된 설명변수 외 다른 설명변수를 고려한다. 남은 설명변수 중에서 F값이 가장 큰 변수를 고려하여 부분F검정을 통해 유의하다는 결과가 나올 경우(귀무가설을 기각한다면) 변수를 추가하고 그렇지 않으면 현재 모형을 유지한다. (X2 외 F값이 갖아 큰 변수를 X4라고 가정하자. 귀무가설 : Y= β0+ β1X2, 대립 가설 : Y= β0+ β1X2+ β2X4으로 부분 F검정을 실시했을 때 귀무가설을 기각하면 X4를 추가하고, 아니면 귀무가설 모형을 유지한다)
3단계 : 추가된 설명변수에 대하여 이번에는 반대의 검정을 실시한다. 2단계에서 실시한 검증은 (1단계에서 추가된 설명변수 대 1단계에서 추가된 설명변수 + 2단계에서 추가된 설명변수)라고 한다면 3단계에서는 (2단계에서 추가된 설명변수 대 1단계에서 추가된 설명변수 + 2단계에서 추가된 설명변수)를 가지고 비교하는 것이다. (귀무가설 : Y= β0+ β1X4
, 대립가설 : Y= β0+ β1X2+ β2X4으로 부분 F검정을 실시했을 때 귀무가설을 기각하면 2단계에서 형성된 모형을 유지하고, 아니면 X2을 제거한다)
단계별 회귀 검정 결과 최적의 모형은 Y= β0+ β1X1+ β2X2+ β3X3 + εi이다.
(사) 전진 선택법
전진 선택법은 단계별 회귀와 비슷하지만, 3단계 과정의 변수를 제거할지 여부를 판별하는 과정을 거치치 않는다. 단계별 회귀에 비해 알고리즘 반복 횟수가 적어 속도가 빠르다는 장점이 있지만, 단점으로는 모든 경우의 수를 고려하지 않아 비교적 정확도가 떨어진다는 단점이 존재한다.
전진 선택법으로 검증한 결과 최적의 모형은 Y= β0+ β1X1+ β2X2+ β3X3 + εi으로 이전 변수 선택의 결과와 크게 다르지 않았다.
(아) 후진 제거법
후진 제거법은 반대로 최대 모형에서 시작하여 설명변수를 삭제해나가는 방법이다. 전진 선택법의 역순이라고 보아도 무방하다. 후진 제거법으로 검증한 결과 최적의 모형은 Y= β0+ β1X1+ β2X2+ β3X3 + εi이다.
따라서 나는 위 변수 선택 결과들을 근거로 Y= β0+ β1X1+ β2X2+ β3X3 + εi을 최적의 모형으로 선택하였다.
② 중회귀모형의 설립
우리는 ① 변수 선택을 통해 Y= β0+ β1X1+ β2X2+ β3X3 + εi 가 최적의 모형임을 확인하였다. 우리는 해당 모형을 가지고 중회귀모형을 구성하였다. 중회귀모형을 구성할 때 이전 단계에서 선택한 3개의 설명변수와 더불어 양적 변수인 X1과 범주형 데이터 변수인 X2, X3과의 교호작용까지 고려하였다. 그 결과는 아래와 같다.

이를 식으로 변환하면 아래와 같이 표현된다. 참고로 Z는 ‘평소 스트레스 인지 정도’와 관련된 영향력이며, D는 ‘2주 연속 우울감 여부’와 관련된 영향력이다.

위 공식의 의미를 정리해보자.
첫째, 다른 변수가 보정되었을 때, 평일 수면시간(X1)이 한 단위 증가하면, 주말 수면시간(Y)은 0.87만큼 증가한다.
둘째, 다른 변수가 보정되었을 때, 평균 스트레스 인지 정도가 ‘거의 느끼지 않는 사람’에 비해
(1) ‘스트레스를 조금 느끼는 사람(Z1)’은 주말 수면시간(Y)이 0.76만큼 많으며, 평일 수면시간(X1)은 0.07만큼 감소한다.
(2) ‘스트레스를 많이 느끼는 사람(Z2)’은 주말 수면시간(Y)이 1.46만큼 더 많으며, 평일 수면시간(X1)은 0.16만큼 감소한다.
(3) ‘스트레스를 대단히 많이 느끼는 사람’은 주말 수면시간(Y)이 1.50만큼 더 많으며, 평일 수면시간(X1)은 0.14만큼 감소한다.
셋째, 다른 변수가 보정되었을 때, 2주 이상 우울감 여부가 ‘아니오’인 사람에 비해 ‘예’인 사람은 주말 수면시간(Y)이 1.38만큼 더 적으며, 평일 수면시간(X1)은 0.16만큼 감소한다.
③ 가설의 검정
앞서 우리는 해당 분석을 진행하기 전에 가설을 세 가지 세워둔 바 있다.
첫째, 주말 수면시간과 평일 수면시간은 서로 반비례의 관계일 것이다.
둘째, 주말 수면시간과 체감 스트레스는 서로 반비례의 관계를 나타낼 것이다.
셋째, 주말 수면시간과 체감 우울감은 서로 반비례의 관계일 것이다.
그러나 실제 분석 결과, 평일 수면시간이 한 단위 증가하면 주말 수면시간도 비례해서 증가하는 것으로 나타났으므로 첫 번째 가설은 기각된다.
두 번째 가설의 경우, 스트레스가 한 단계씩 증가할 때마다 주말 수면시간이 각각 0.76, 1.46, 1.50만큼 증가하는 것으로 나타났으므로, 두 번째 가설 또한 기각한다.
세 번째 가설은 ‘2주 이상 우울감 여부’가 ‘아니오’인 사람에 비해 ‘예’인 사람은 주말 수면시간이 1.38만큼 적어지는 것으로 나타나 세 번째 가설은 채택한다.
(2) 회귀모형의 검정
회귀분석은 회귀모형을 구성하는 것보다 회귀모형을 검정하는 단계가 더욱 중요하다. 회귀분석에는 수많은 전제 위에서 분석이 진행되는데, 이 중 하나라도 틀어질 경우, 아무리 회귀계수가 유의하다고 나타나더라도 그것을 올바른 회귀모형이라 이야기하기 힘들어진다. 따라서 회귀모형의 철저한 검정과 함께, 가정이 올바르지 않을 경우 적절한 조정을 거쳐 최대한 가정에 부합하도록 만들어주는 과정이 반드시 필요하다. 다만 나의 경우 ‘학부생’ 단계의 회귀분석만 배웠으므로 많은 내용을 적용하여 기말 프로젝트를 진행할 수는 없었다.
④ 회귀계수의 검정
우리는 일전에 아래와 같은 회귀모형을 구성한 바 있다.

여기에 적힌 회귀계수를 모두 beta_i의 형태로 변경한다.
Yi= β0 + β1X1 + β2Z1 + β3Z2 + β4Z3 + β5D + β6X1Z1 + β7X1Z2 + β8X1Z3 + β9X1D + εi
우리는 해당 회귀계수가 유의한지를 살펴보기 위하여
귀무가설 : βi=0, 대립가설 : βi ≠0 로 설정하여 회귀계수에 대한 t검정을 실시하였다.

그 결과, 모든 회귀계수의 p값이 0.05를 넘지 않는 것을 확인할 수 있다. 즉 귀무가설을 기각하므로, 내가 세운 회귀모형의 계수가 모두 유의하다는 사실을 확인할 수 있다. 사실, 회귀계수가 유의한지 아닌지는 회귀계수의 신뢰구간으로도 확인이 가능하다.

위 이미지는 모든 회귀계수의 신뢰구간을 산출한 결과이다. 내용을 살펴보면 어느 구간에서도 “0”을 포함하지 않는다는 것을 알 수 있다. 이는 귀무가설 βi=0 과도 맞지 않으므로 자연스럽게 귀무가설은 기각된다.
④ (보고서 작성 시 삭제된 항목) 편회귀그림에 의한 영향력 검증
편회귀그림은 표본편상관계수를 이용한 그래프를 통해 설명변수의 순수한 영향력을 확인하는 방법이다. 표본편상관계수는 측정하고자 하는 설명변수를 X1이라고 가정했을 때, (X1을 제거하고 구성한 회귀모형의 잔차)와 (X1을 반응변수로 둔 후에 구성한 회귀모형의 잔차) 간의 상관계수를 말한다. 지금부터 표본편상관계수의 식이 이와 같이 구성되는 이유를 설명해보고자 한다.
설명변수가 X1부터 X3까지 총 세 개가 존재한다고 가정한다. X1을 제거하고 구성한 회귀모형을 말로 풀어보면 ‘X2와 X3로 설명한 Y’이다. 그리고 이러한 회귀모형의 잔차는 ‘X2와 X3로 설명되지 못한 Y값’이라고 설명할 수 있다. 그런데 우리는 X1을 제거하고 회귀모형을 구성한 바 있으므로 X2와 X3으로 설명되지 못한 Y값은 곧 X1을 의미하게 된다.
그러나 위의 설명만으로도 부족한 감이 있다. 왜냐하면, X1에 포함된 X2, X3의 영향력을 제거하지 못했기 때문이다. 우리는 이 부분을 보정하기 위하여 X1을 반응변수로 설정하여 회귀모형을 구성한다. 이렇게 세워진 회귀모형을 말로 풀어서 설명하면 ‘X2와 X3으로 설명한 X1’이다. 그런데 이 회귀모형의 잔차는 곧 ‘X2와 X3으로 설명되지 못하는 X1’라고도 볼 수 있을 것이다. X2와 X3으로도 설명되지 못하는 X값이란 곧 순수한 X1이라고 치환해서 생각할 수 있다. 따라서 이 둘의 상관계수는 바로 순수한 X1의 영향력을 표현한, X1의 표본편상관계수가 된다. 그리고 X1의 표본편상관계수를 그래프로 그리면 그것이 바로 X1에 대한 편회귀그림이다.
범주형 데이터의 경우, 표본편상관계수를 구하기 쉽지 않다(사실 가능한지, 아닌지조차 잘 모르겠다). 그러므로 내 수준에서는 범주형 데이터가 아닌 설명변수를 가지고 표본편상관계수를 구한 뒤 이를 그래프로 그려보았다. 그 결과는 아래 그림과 같다.
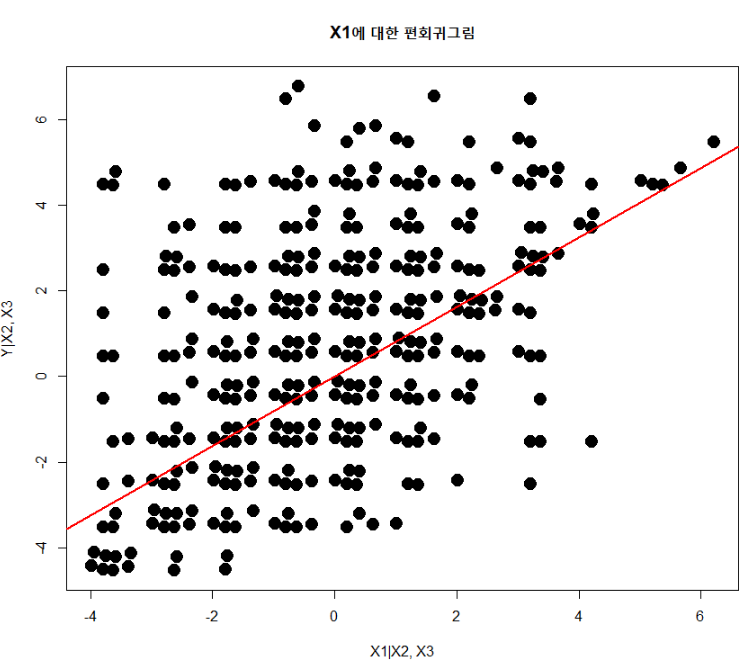
|
Call:
lm(formula = NotX1resid ~ YisX1resid) Coefficients: (Intercept) YisX1resid -2.713e-15 8.129e-01 |
편회귀그림 결과, X1의 순수한 영향력은 0.8129라는 사실을 알 수 있다. 편회귀그림의 단순회귀식에서 기울기는 완전 모형에서 보정된 X1의 기울기를 의미한다. 그리고 이 값은 중회귀모형의 X1값과 동일해야 한다. 그런데 우리가 이전에 세워둔 회귀모형의 X1계수는 0.87로 여기서 말하는 0.812와 많은 차이를 보이고 있다. 이에 대해서는 아래 값을 본다면 이해할 수 있다.
|
Call:
lm(formula = Y ~ X1 + factor(X2) + factor(X3), data = Hn_full) Coefficients: (Intercept) X1 factor(X2)1 factor(X2)2 factor(X2)3 factor(X3)1 1.7589 0.8129 0.2389 0.3874 0.5160 -0.2832 |
위 결괏값은 교호작용을 “포함하지 않은” 경우의 회귀계수 값이다. X1을 살펴보면 0.8129로 우리가 편회귀그림으로 추정한 값과 동일하다. 이는 즉, 편회귀그림에서 추정한 회귀계수의 경우 교호작용이 포함된 중회귀분석의 X1 영향력을 정확히 측정해주지 못한다는 사실을 말해준다. 따라서 나는 기말 프로젝트 보고서를 작성할 때 편회귀그림과 관련한 부분은 모두 삭제하였다.
⑤ 적합결여검정
그림을 이용한 적합결여검정에서 설명변수가 1개일 경우에는 (1) 잔차의 산점도를 활용하거나, (2) Y값과 추정된 Y값 간의 산점도를 이용하거나, 혹은 (3) 적합된 회귀식과 LOESS 평활곡선끼리 비교하는 방법이 있다. 다만 중회귀분석의 경우 설명변수가 1개를 넘어가기 때문에 이러한 방식을 사용하는 것은 힘들뿐더러, 애초에 그림을 이용한 적합결여검정은 직관적으로 확인하기 어려울 것이라 생각하여 나는 사용하지 않았다. 만약 중회귀분석이면서 그림을 이용한 적합결여검정을 활용하고 싶다면 위에서 설명한 편회귀그림을 활용하여 비교할 것을 추천한다.
그래서 나는 두 번째 방법인 ‘분산을 이용한 적합결여검정’을 활용하기로 하였다. 만약 적합한 회귀식 A가 존재하는데, 우리는 적합한 회귀식에서 설명변수 하나를 더 추가하여 회귀식 A’을 구성하였다고 가정해보자. 이 경우 Y의 값과 추정된 Y값(Y_hat) 사이의 격차는 점차 커질 것이다. 이것은 SSE(sum((Yi- Yi_hat)^2)) 의 값이 커지는 결과로 이어지며, MSE = (SSE / n-2)= {sum((Yi- Yi_hat)^2)} / n - 2= s^2 (단, n – 2는 자유도)의 값이 커지는 결과로 이어진다. 즉, MSE의 값이 과대 추정될 경우, 해당 공식에서 사용된 변수가 적합하지 않다는 것을 의미할 수 있다. 분산을 이용한 적합결여검정은 이러한 원리를 이용한 방법이다.
R에서 분산을 이용한 적합결여검정을 실시할 때는 수치자료를 범주형 데이터로 변경한 뒤, Y의 반복 관측값을 사용하여 추정한다. 나는 이미 범주형 데이터인 X2와 X3은 적합결여검정에서 적절하지 않다고 판단하였고, 따라서 일반 수치자료인 X1만을 가지고 적합결여검정을 실시하였다. 귀무가설은 Yi= β0+ β1X1, 대립가설은 Yi≠ β0+ β1X1로 설정한 후 검정을 실시한 결과는 아래와 같다.

위를 살펴보면 0.05를 넘지 못하므로 귀무가설 Yi= β0+ β1X1 이 기각되는 것을 알 수 있다. 이는 설명변수 X1이 적합하지 않다는 것을 보여준다.
⑥ 분산 및 정규성의 안정화를 위한 변수 변환
가. 분산 안정화를 위한 변수 변환

우리가 구성한 회귀모형의 잔차를 그래프로 나타낸 것이다. 잔차의 추이를 보여주는 붉은 선이 수평에 가깝게 그려져 있다고는 하나(수평의 형태를 띨수록 잔차의 분포가 고르다고 말한다), 이것만으로 ‘그래프의 상태가 좋다’라고 이야기하기에는 부족한 점이 많다고 생각하였다. 그 이유로는 (1) 잔차의 퍼짐 정도가 -5부터 5까지 상당히 넓게 분포되어 있다는 점, 그리고 (2) 잔차의 분포가 일자로 분포되어 있는 것이 아닌, 대각으로 내려가는 듯한 모습을 보여주기 때문이다. 따라서 나는 분산 안정화를 위한 변수변환을 진행하기로 결정하였다.
분산안정화를 위하여 변수를 변환하는 방법은 분산 함수와 평균 함수와의 관계에 따라 각각 다른 방식을 적용한다. 그러나, 나는 편의를 위하여 대표적인 변수변환방법인 sqrt_Y, log_Y, inv_Y를 사용하여 (1) 모든 변수가 유의한지를 확인한 후, (2) 잔차의 분포를 살펴보는 단계로 분석을 진행하였다.
(가-1) 모든 변수가 유의한가
먼저 나는 R에서 제공하는 함수를 이용해 모든 변수가 유의한지를 확인해보았다.


가장 좌측 상단부터 순서대로 원본 모형, log_Y모형, sqrt_Y모형(좌측 하단), inv_Y모형이다. 유의 수준은 0.05로 두고 판단하였다. 모든 경우의 수에서 변수 변환을 한 이전보다, 이후에 수정된 결정계수 값이 소폭 상승하는 효과를 얻을 수 있었다. 그러나 log_Y모형과 inv_Y모형에서는 몇 가지 변수가 유의하지 않게 나오는 것을 확인할 수 있었다. 그러나 유일하게 sqrt_Y모델은 모든 변수가 유의하다는 결과를 얻을 수 있었다. 따라서 나는 sqrt_Y모형을 후보군으로 놓고 원본 모형과 그래프를 비교해본다.
(가-2) 그래프의 추이 확인

위 사진에서 좌측 4개의 그래프는 원본 모형을 가지고 그린 그래프이며, 우측 4개는 sqrt_Y모형을 가지고 그린 그래프이다. 아쉽게도 각 그래프의 좌측 상단에 위치한 잔차 그래프에서는 유의미한 변화를 확인할 수는 없었다. 그러나 각 그래프의 좌측 하단에 위치한 Scale-Location 그래프의 붉은 선 추이가 원본 모형과 비교했을 때 비교적 수평에 가까운 형태로 바뀐 것을 알 수 있다. 따라서 나는 sqrt_Y모형을 채택하였다.
sqrt_Yi= β0+ β1X1+ β2Z1+ β3Z2 + β4Z3 + β5D + β6X1Z1+ β7X1Z2+ β8X1Z3+ β9X1D+ εi
(나) 정규성을 만족시키기 위한 변수 변환

오차항의 정규성을 확인하는 가장 대표적인 방법은 QQplot을 활용하는 것이다. 만약 QQplot이 QQline(붉은 선)을 잘 따라가고 있으면, 우리는 오차항의 정규성이 충족되었다고 말한다. 만약 그렇지 않으면 오차항의 정규성을 충족했다고 말하지 못하며, 회귀모형의 전제는 무너진다.
위 그래프는 원본 모형으로 QQplot을 그려본 결과이다. 위 사진에서도 알 수 있듯 QQplot이 초반부와 마지막 부분에서 QQline을 크게 벗어났음을 확인할 수 있다. 나는 이를 근거로 현재 모형이 정규성을 만족하기 어렵다고 판단하였고, Box&cox변환을 사용하여 의미 있는 람다 값을 찾아 변수를 변환해보았다.

박스 칵스 변환 결과, 람다 값(Y값에 적용할 지수)은 0.67이 나온 것을 확인할 수 있다. 나는 0.67과 가장 근접한 0.7을 후보군 1로, 그리고 0.67을 1로 반올림한 모형(원본 모형)을 후보군 2로 둔 후 QQplot을 비교해보았다.

좌측이 후보군 1, 우측이 후보군 2이다. 위 그래프를 보다시피 QQplot이 개선되는 모습은 보이지 않았다. 따라서 나는 sqrt_Y만 적용한 모형을 최종 모형으로 선택하였다.
⑦ 다중공선성의 탐색과 조정
다중공선성을 탐색하기 이전에 본래는 ‘표준화회귀계수 = {sum(Yi- Y_bar)} / {sqrt(sum((Yi- Yi_bar)^2))} (대표적으로 Y만 적은 것일 뿐, 표준화회귀계수를 구하기 위해서는 모든 설명변수에도 같은 과정을 적용해야 한다)’를 통해서 각 데이터 값 ‘단위(kg과 g, km와 m, mm 등)’의 영향력을 최소화하는 과정을 거친다. 그러나 내가 사용한 변수의 단위는 모두 ‘시간’으로 동일하므로 표준화 과정을 거치지 않고 곧바로 다중공선성 탐색과정을 진행하는 것이다.
다중공선성을 탐색하는 방법으로는 두 가지가 있는데, 하나는 각 설명변수 간 표본상관관계값을 조사하는 방법이다. 표본상관계수행렬을 도출한 다음, 설명변수 간 표본상관관계값이 0.8이상인 값을 찾는다. 일반적으로 0.8 이상이면 다중공선성을 의심하고, 0.9 이상이면 다중공선성의 가능성이 있다고 판단하지만, 연구자에 따라 혹은 상황에 따라 0.8을 넘지 않더라도 다중공선성을 의심하고 값을 수정하는 경우도 있다.
다른 하나의 방법은 가장 보편적인 방법으로 분산팽창인수(VIF)값으로 확인하는 방법이다. 분산팽창인수의 원리는 X1을 반응변수로 두고, 나머지 설명변수로 회귀분석을 진행한 다음, 산출된 회귀식으로 결정계수 값을 산출한다. 이 산출된 결정계수 값을 바탕으로 1 / (1- R^2) 의 공식을 이용해 지수를 확정한다. 일반적으로 VIF값이 5 이상(1/(1-0.8) = 1/0.2 = 5)이면 다중공선성을 의심할 수 있고, 10보다 크면 다중공선성의 가능성이 있다고 판단한다고 하나, 위에서 말했듯 연구자 혹은 상황에 따라서 5를 넘지 않더라도 다중공선성을 의심하고 값을 처리할 수 있다. 만약 표본상관관계값 혹은 VIF값이 높다고 판명날 경우 연구자는 두 개의 선택을 할 수 있다. 값이 높은 두 설명변수 중 하나만 적용하거나, 혹은 부분 F검정을 통해서 두 개의 설명변수 중 하나를 고른다.
나는 여기서 문제가 하나 더 있었는데, 그것은 바로 모든 변수가 수치형이 아니다 보니 VIF값이 제대로 나오지 않았던 것이다. 이것에 대해 나는 교수님과 상담을 진행했고, VIF검정을 진행할 때는 모든 설명변수를 수치자료로 간주하여 VIF검정을 진행하기로 결정하였다. 물론 내가 아직 학부생이기도 하다 보니 간편한 방식을 알려주신 것일 수도 있다. 실제로 내가 인터넷 검색을 했을 때는 GVIF와 같은 내용을 찾을 수 있었기 때문이다. 따라서, 이 글을 읽고 있는 여러분이 만약 비슷한 문제를 마주하게 된다면 교수님께 질문해서 적절한 답을 찾기를 바란다.
⑧ 잔차 검정
잔차 검정 파트에서는 여러 측도를 활용하여 영향력 관측치 및 지렛값을 확인하고, 필요하면 데이터 값을 일부 제거하여 재검정 하는 방식을 사용한다. 이를 통해 가정에 걸맞은 잔차 분포를 유도하여 회귀모형의 안정화를 꾀하도록 한다.
(가) 표준화잔차를 이용한 특이점 확인
잔차란 실제 반응변수의 값과 회귀모형을 통해 추정된 반응변수의 값의 차이를 말한다. 일반적으로 우리는 회귀모형을 세울 때 (1) 오차항의 평균은 0이며, (2) 분산은 sigma^2, (3) 그리고 독립인 확률변수”라고 가정한다. 하지만 오차항이 실제 어떤 값인지 우리가 추정하기란 쉽지 않다. 따라서 우리는 회귀모형으로 이용해 추정한 반응변수와 실제 반응변수 간 차이를 이용해 오차항을 간접적으로 추정하고자 하는 것이다. 다만 잔차는 정규분포를 따를지는 몰라도 오차항의 전제와 달리 독립성, 등분산성은 만족되지 않는다. 잔차 하나하나는 독립성, 등분산성을 만족되지 못하더라도, 잔차는 오차항의 현실화한 값이니 전반적인 잔차의 분포형태를 살펴보고 독립성, 등분산성을 판단하는 것이다.
다만 잔차도 단위에 많은 영향을 받기 때문에 표준화를 시켜주어야 할 필요가 있다. 그래서 나는 표준화잔차를 관측 순서에 따라 분포도를 그린 뒤 -2부터 2까지 붉은 선으로 표시를 해주었다. 이때 -2부터 2까지 표시를 한 이유는 일반적으로 해당 구간을 벗어난 값을 특이값으로 보기 때문이다.

위 결과를 보시다시피 구간을 넘어가는 데이터의 개수가 상당히 많음을 알 수 있다. 특이값의 개수를 확인한 결과 343개가 출력되었다.
(나) 기타 측도에 의한 특이값 및 지렛값 계산
| 영향력 측도 | 기준변수 | 영향력 관측치(개) |
| leverage | - | 3134 |
| Cook’s distance | - | 413 |
| DFBETAS | X1 | 264 |
| Factor(X2).1 | 313 | |
| Factor(X2).2 | 356 | |
| Factor(X2).3 | 259 | |
| Factor(X3).1 | 315 | |
| X1.factor(X2).1 | 207 | |
| X1.factor(X2).2 | 267 | |
| X1.factor(X2).3 | 249 | |
| X1.factor(X3).1 | 271 | |
| DFFITS | - | 1192 |
| COVRATIO | - | 4993 |
위 표는 각 측도에 의해서 나타난 특이값 혹은 지렛값을 정리한 것이다. 지금부터 하나씩 짚어보면서 각 측도가 어떤 의미를 가지고 있는지를 설명하도록 한다.
먼저 지렛값(leverage)은 평균값을 중심으로 멀리 떨어져 있는 관측치를 의미한다. 지렛값은 회귀모형의 기울기에 영향을 주어서 왜곡시킬 수 있는 만큼 관심 있게 지켜보아야 할 값이기도 하다. 2p / n을 기준으로 판단하는데, 여기서 n은 데이터의 개수이며 p는 설명변수의 개수를 의미한다. 뒤에서 나올 모든 기준점에서도 동일한 의미를 가진다.
쿡의 거리(Cook’s distance)는 beta에 대한 i번째 관측치의 영향력이 얼마나 큰지를 판단하는 척도이다. (모든 자료를 이용하여 beta를 측정한 값)에서 (i번째 관측치의 자료를 제외한 나머지 자료를 이용하여 beta를 측정한 값)이 3.67 / n-p를 넘어가면 특이값으로 판단한다.
DFBETAS란 ‘Difference in betas’의 약자로, “i번째 관측치가 j번째 회귀계수에 영향을 얼마나 주느냐”에 따라서 특이값을 판단한다. 기준은 2 혹은 2 / sqrt(n)을 사용하는데, 이번 측정에서는 2 / sqrt(n)을 사용하였다. j번째 회귀계수에 얼마나 영향을 주는지를 판단하기 때문에, 모든 회귀계수를 따로따로 측정하게 된다.
DFFITS는 ‘Difference in Standardized Fits’의 약자로, “i번째 관측치가 추측된 반응변수의 결괏값에 얼마나 영향을 미치는지”에 따라 특이값을 판단한다. 특이값 기준은 2 / sqrt(p / n)이다.
마지막으로 COVRATIO는 말 그대로 “공분산 beta_hat의 추정 값에 대하여 i번째 관측치가 얼마나 영향력이 있는가”를 두고 특이값을 측정한다. 특이값 기준은 abs(COVRATIO_i - 1) ≥ 3p / n이다.
위에서 각 영향력 측도를 설명한 부분을 보고 여러분들도 눈치챘듯이 사실 나도 영향력 측도와 관해서는 많은 부분은 알지 못한다. 그래서 구체적인 해석까지는 할 수 없었고, 대신 특이값 및 지렛값의 개수만 표시해둔 것이다.
위 값들을 보면 적게는 200개부터 많게는 5000개까지 나타난 것을 확인할 수 있다. 특이값을 모두 제거한다면 좋겠지만, 그렇게 진행하면 원본 데이터에 손상이 갈 만큼 많은 양을 지워야 하기 때문에 위 척도를 활용하지 못했다. 대신 차선책으로 표준화잔차를 기준으로 자료의 10%가량을 제거한 후 잔차를 재검정하기로 결정하였다.
⑨ 이상치 제거 후 잔차의 재검정
이전까지 나는 6648개의 데이터를 가지고 분석을 진행하였다. 그러나 표준화잔차를 기준으로 자료의 10%가량 제거한 뒤에 잔차를 재검정하기로 결정한 이상 약 600개의 데이터 삭제가 불가피하다. 그래서 나는 표준화잔차의 기준치(-2, 2)에서 가장 멀리 떨어진 값부터 600번째 값까지 출력한 후 직접 확인해보았는데, 값이 중복되어 삭제 대상 데이터가 600개를 넘어버리고 있었다. 그래서 중복된 값도 모두 포함하여 삭제 대상이 포함한 결과 632개가 삭제되었고, 삭제 후 데이터의 개수는 6016개가 되었다.
가. 변경된 표준화잔차

표준화잔차를 기준으로 특이값을 삭제하다보니 분포가 많이 안정화된 모습을 보이고 있었다. 그러나 아직까지도 기준선 -2~2를 넘어서는 값들이 많이 발견되고 있었다. 이전 표준화잔차에서 발견한 특이값이 343개이고, 삭제한 데이터가 632개나 되고 있음에도 표준화잔차가 완벽하게 잡히지 않은 이유는 표준화잔차 공식에 자료의 개수 n이 포함되어 있어 표준화잔차 값이 달라졌기 때문으로 추측된다.
나. 변경된 특이값 및 지렛값
| 영향력 측도 | 기준변수 | 영향력 관측치(개) | 증감(개) |
| Leverage | - | 2817 | -317 |
| Cook’s distance | - | 375 | -38 |
| DFBETAS | X1 | 137 | -127 |
| Factor(X2).1 | 249 | -64 | |
| Factor(X2).2 | 314 | -42 | |
| Factor(X2).3 | 209 | -50 | |
| Factor(X3).1 | 233 | -82 | |
| X1.factor(X2).1 | 280 | +73 | |
| X1.factor(X2).2 | 364 | +97 | |
| X1.factor(X2).3 | 194 | -55 | |
| X1.factor(X3).1 | 221 | -50 | |
| DFFITS | - | 994 | -198 |
| COVRATIO | - | 4407 | -586 |
전반적으로 특이값이 많이 감소했기는 하나, 일부 특이값은 오히려 증가한 것을 확인할 수 있었다.
다. 변경된 분포

삭제된 데이터를 바탕으로 다시 분포도를 그려본 결과는 위와 같다. 잔차도의 경우, 데이터의 분산이 이전보다도 더욱 안정화되었으며, QQplot도 QQline을 따라 움직이려는 모양으로 변경된 것에 큰 의의가 있다. 여기서 잔차의 세로축이 -0.4부터 0.4로 바뀌었는데, 이것은 이전 변수 변환 파트에서 Y를 sqrt_Y로 변경하는 과정에서 세로축이 바뀌었을 가능성도 있으므로 유의미한 결과로 포함시키지 않는다. 그 외 나머지 그래프는 큰 변화가 발생하지 않은 것을 확인할 수 있다.
지금까지 우리는 잔차 검정을 통한 회귀모형 전제의 확인을 진행해보았다. 6648개로 분석한 회귀모형의 경우 오차항의 등분산성, 정규성 등 오차항과 관련된 전제가 상당부분 충족되지 않는 것을 확인할 수 있었다. 그래서 나는 안정된 회귀모형을 얻기 위하여 여러 척도를 통해 특이값 및 지렛값을 확인한 후, 표준화잔차를 이용해서 특이값을 삭제하기로 결정하였다.
표준화잔차 -2 ~ 2 범위에서 크게 벗어난 값 632개(대략 10%가량)의 값을 제거한 이후 다시 잔차검정을 진행한 결과 특이값도 어느 정도 안정되었으며 잔차분포도나 QQplot 등 여러 그래프도 상당 부분 개선되는 효과를 얻을 수 있었다. 그러나 오차항의 전제를 충족되었다고 보기에는 많이 부족하다고 결론을 내렸다.
⑩ 예측력 판단
예측력을 판단하는 방법은 (1) SSE와 PRESS를 비교하는 방법, 그리고 (2) 1 – (SSE/SST)와 1 – (PRESS/SST)를 비교하는 방법 두 가지가 있는데, 두 방법 모두 SSE를 활용한다는 공통점이 있다. SSE는 sum((Yi - Yi_hat)^2)로 (실제 Y값)에서 (추정된 Y값)의 차이며, PRESS는 sum((Yi - Yi(i)_hat)^2)로 (실제 Y값)에서 (i번째 자료값을 제외한 뒤 추정한 Y값)의 차이다. 만약 회귀모형의 예측력이 좋다면 (추정된 Y값)과 (i번째 자료값을 제외한 뒤 추정한 Y값)에 차이가 작을 것이기 때문에 SSE와 PRESS 간 차이가 작을 것이라고 말할 수 있는 것이다.
PRESS와 SSE 값을 비교한다고 가정했을 때, PRESS = 4041.639이고 SSE는 4029.618이므로 거의 비슷하다고 할 수 있다. 또 결정계수 값을 비교했을 때도 1 – (SSE / SST) = 0.6998829, 1 – (PRESS / SST) = 0.6989876으로 거의 차이가 없는 것을 확인할 수 있었다. 따라서 회귀모형의 예측력은 상당히 괜찮다는 사실을 알 수 있다. 다만, 여기에는 특이값 632개를 삭제하는 과정에서 회귀모형의 예측력이 개선된 영향도 포함되었을 가능성이 있다.
Ⅲ. 결론
지금까지 우리는 응답자의 평일 수면시간과 체감 스트레스, 체감 우울감이 주말 수면시간에 미치는 영향 분석이라는 주제로 회귀분석을 진행하였다. 그 결과 평일 수면시간과 체감 스트레스는 주말 수면시간에 비례하였으나, 반대로 체감 우울감과는 반비례한다는 사실을 알아낼 수 있었다.
그러나 회귀모형을 검증하는 과정에서 많은 문제가 발생하였다. 회귀계수, 혹은 다중공선성, 예측력 등에서는 준수한 모습을 보여주었지만, 반대로 적합결여검정이나 잔차 검증 부분에서는 이상적인 결과를 얻어낼 수 없었다. 특히 잔차 검증의 경우, 특이값을 제거한 이후에도 부적합한 모습이 보이기도 하였다.
위와 같이 회귀모형 자체가 오차항의 전제 등을 충족하지 못하는 모습을 보여주는 이유가 무엇일지 고민해보았다. 그리고 내가 구성한 회귀모형의 설명변수가 반응변수를 잘 설명해주지 못했기 때문이 아닐까 하는 결론에 이르렀다. (1) 수정된 결정계수가 많이 낮은 편이었으며, (2) 표준화잔차의 분포가 넓게 퍼져있었다는 점을 근거로 회귀모형의 예측력 부분에서 문제가 발생한 것이라 생각한 것이다. 따라서 다시 연구를 진행할 기회가 생긴다면 ‘주말 수면시간’을 잘 설명해줄 수 있는 변수를 추가하여 자료조사부터 진행한다면 좋지 않을까 생각한다.
5. 프로젝트를 마치며
본래 정리하고자 했던 부분에 기말 프로젝트 보고서에 넣지 못했던 부분을 추가하고, 각 파트가 의미하는 바를 잊지 않기 위해 추가하니 정리 보고서가 매우 길어졌다. 정리만 했는데도 꼬박 이틀이 소모되었는데, 다시 기말 과제를 하는 것 같은 느낌을 받을 정도로 힘들었다. 그렇지만 회귀분석은 데이터 분석에서 중요한 부분을 차지하기도 하고, 한 학기라는 짧은 시간 안에 귀중한 내용을 많이 배웠던 만큼, 절대로 잊고 싶지 않았기 때문에 더욱 노력해서 자료를 정리했다. 단, 여기에 정리한 내용이 무조건적으로 정답이라는 생각을 가지지 않았으면 한다. 회귀분석은 학부 수준에서는 많이 배우지 않을뿐더러, 자료를 정리하는 지금도 내가 회귀분석 도구를 정확하게 이용했는지조차 모르기 때문이다. 따라서 회귀분석을 배우는 사람이 이 글을 읽게 될 경우, 맹목적으로 내가 정리한 내용을 따라가지 말고 교수님에게 회귀분석과 관련된 내용을 거듭 질문하며 자신만의 분석 틀을 잡아갔으면 한다.
'전문지식 함양 > 학습내용 정리' 카테고리의 다른 글
| [공모전] 2021년 KOSAC 대학생 광고대회 참가 후기 (0) | 2021.12.28 |
|---|---|
| [대학수업] 서비스마케팅 (0) | 2021.12.27 |
| [대학수업] 디자인경영 (0) | 2021.12.22 |
| [교육] 코로나19에도 유망한 산업으로 예상되는 S사의 상품 판매 전략 계획 구상 (0) | 2021.09.13 |
| [공모전] M사 샴푸의 한국 출시 관련한 마케팅 실행 보고서 (0) | 2021.09.07 |